RNG
RNG or Random Number Generation is the game's method of generating a pseudorandom short. By doing this, the game can make things like dust movement seem random[1].
Technical description
The RNG variable is a short, which is a number from 0 to 65535 inclusive. When an object, snow, or something else wants to call RNG, it takes the current RNG value and runs it through the RNG function, below. It uses the result in its own calculations and also stores the result to the RNG variable. Thus, the RNG variable is equal to the last used RNG value. Every frame, every object is iterated through in order of object slots and may choose whether to call RNG once, multiple times, or not at all.
The RNG function
unsigned short rng_function (unsigned short input) {
if (input == 0x560A) input = 0;
unsigned short S0 = (unsigned char)input << 8;
S0 = S0 ^ input;
input = ((S0 & 0xFF) << 8) | ((S0 & 0xFF00) >> 8);
S0 = ((unsigned char)S0 << 1) ^ input;
short S1 = (S0 >> 1) ^ 0xFF80;
if ((S0 & 1) == 0) {
if (S1 == 0xAA55) input = 0;
else input = S1 ^ 0x1FF4;
}
else input = S1 ^ 0x8180;
return (unsigned short)input;
}
Description
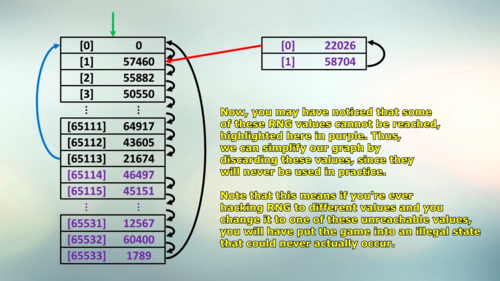
The function has 65536 possible inputs and 65536 possible outputs. It is a bijection, meaning that every input maps to exactly one output and none repeat or are left out. The function forms two loops, one of length 65534 and one of length 2, but one of the if statements causes the cycle of 2 to lead back to the cycle of 65534. Oddly, the RNG value of 21674 at index 65113 loops back to index 0. This may be because this index's S1 value is equal to the previous RNG value for the first time, but that is no reason to prematurely end the loop. Indeces 65114-65533, as well as values 22026 and 58704 (the loop of 2, which are not given indeces) are considered impossible RNG values and cannot be reached without hacking. All other RNG values are considered possible RNG values. The RNG index and value of 0 is set when the game powers on.
Cycling RNG
Because RNG indeces loop from 0 to 65113 and back to 0 again, by looping through every RNG index Mario can reach any reachable RNG value. By making dust, Mario can advance RNG 4 times per frame, which takes 9 minutes to loop. If objects are calling RNG, this time will be much faster.
Objects that call RNG
The following objects always call RNG under the given circumstances.
- Dust calls RNG to determine its resultant angle and horizontal speed. Note that the dust itself calls RNG, not the dust spawner.
- Goombas call RNG to determine which direction to move when they do not see Mario.
- Bob-ombs call RNG almost every frame to determine whether to blink. If the value that they receive is less than 656, they blink. Otherwise, they don't. Taking into account impossible RNG, the chance of a Bob-omb blinking on a given frame is 0.0099785.
- Although not an object, snow also calls RNG.
- Coins from Bob-ombs, Goombas, Big Cork Boxes, Cork Boxes, Piranha Plants, Bullies, Chuckyas, Fly Guys, Snowmen, etc... you name it, it calls RNG 3 times to determine angle, horizontal speed, and vertical speed. Since angles are shorts just like RNG, the RNG value is used directly for the angle. Horizontal speed is set to (RNG / 65536) * 20, and vertical speed is set to (RNG / 65536) * 40 + 17. Since these RNG calls must be contiguous, there are still only 65114 possible coin trajectories.
- Bowser calls RNG to determine which attack to do next.
- And many, many, many more.
Tick Tock Clock Random Setting Only
The following objects call RNG under the given circumstances when the clock was entered at 6:00 (the random setting).
- Spinners call RNG twice when they stop spinning[2]. The first call determines direction. If the result is less than 32768, the spinner spins clockwise, and otherwise counterclockwise. The second call determines intended angular displacement. Spinners calculate their intended angular displacement by the following formula, in which % denotes the modulo function:
Intended Angular Displacement = (RNG % 4) * 30 + 30
The following is a table summarizing this information, with probabilities of the individual states in parentheses:
| Spinner intended CW ang disp (AU) | RNG2 % 4 = 0 (24.982339%) | RNG2 % 4 = 1 (24.999232%) | RNG2 % 4 = 2 (25.008447%) | RNG2 % 4 = 3 (25.009982%) |
|---|---|---|---|---|
| RNG1 ≥ 32768 (49.983107%) | -30 (12.485794%) | -60 (12.490401%) | -90 (12.501152%) | -120 (12.505759%) |
| RNG1 < 32768 (50.016893%) | 30 (12.496545%) | 60 (12.508831%) | 90 (12.507295%) | 120 (12.504223%) |
- Cogs call RNG twice when they reach their target angular velocity (TAV)[3]. The cog approaches its TAV with an angular acceleration of ±50AU/frame². The first call determines the cog's next TAV. Because of the way the formula is structured, there is a possibility that the TAV is 0. If this occurs multiple times, the cog can stand still. The TAV is calculated by the following formula:
Target Angular Velocity = (RNG % 7) * 200
The second RNG call determines the sign of the TAV. If the result is less than 32768, the sign is -1, and 1 otherwise.
The following table summarizes this information:
| RNG1 % 7 | 0 (14.313358%) | 1 (14.265749%) | 2 (14.278035%) | 3 (14.281107%) | 4 (14.282643%) | 5 (14.284179%) | 6 (14.284929%) |
|---|---|---|---|---|---|---|---|
| RNG2 < 32768 (50.016893%) | 0 | -200 (7.1274995%) | -400 (7.1413214%) | -600 (7.1490002%) | -800 (7.1443929%) | -1000 (7.1505360%) | -1200 (7.1490002%) |
| RNG2 ≥ 32768 (49.983107%) | 0 | 200 (7.1382498%) | 400 (7.1367141%) | 600 (7.1321068%) | 800 (7.1382498%) | 1000 (7.1336425%) | 1200 (7.1459287%) |