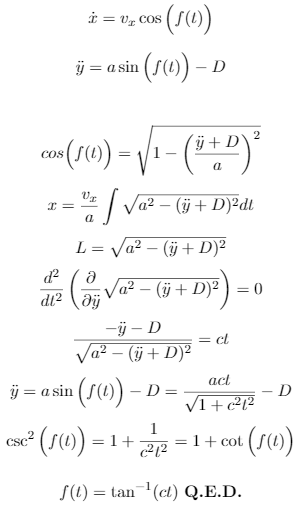Iwerlipse: Difference between revisions
Jongyon7192p (talk | contribs) No edit summary Tags: Mobile edit Mobile web edit |
m (Change Ellie's (Silverstrawb's) name as per her request.) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
The Iwerlipse is the range of positions Mario can occupy when Mario is in the air and cannot turn, assuming the joystick input polling were continuous. It is defined as an area bounded by a shape drawn by the solution to optimizing a set of 2 differential equations. Due to the shape being similar to a superellipse (after Grassdigger brute forced for the solution in Mathematica), Pannenkoek2012 proposed calling this shape the "Iwerlipse" on August 2018 (pronounced eeverlipse /ˈivɜlɪps/) as a pun on the name of Iwer Sonsch, one of the people involved in this problem. | The '''Iwerlipse''' is the range of positions Mario can occupy when Mario is in the air and cannot turn, assuming the joystick input polling were continuous. It is defined as an area bounded by a shape drawn by the solution to optimizing a set of 2 differential equations. Due to the shape being similar to a superellipse (after Grassdigger brute forced for the solution in Mathematica), Pannenkoek2012 proposed calling this shape the "Iwerlipse" on August 2018 (pronounced eeverlipse /ˈivɜlɪps/) as a pun on the name of Iwer Sonsch, one of the people involved in this problem. | ||
| Line 21: | Line 21: | ||
Iwer stated on April 2018 that optimal straining for the Air_no_Turn action is <math>\text{dyaw}(t,r) = \text{acotan}(0.15r*t) </math>. | Iwer stated on April 2018 that optimal straining for the Air_no_Turn action is <math>\text{dyaw}(t,r) = \text{acotan}(0.15r*t) </math>. | ||
On October 2019, | On October 2019, Silverstrawb provided a full analytical proof for Iwer's claim, using a generalized 2nd-order Euler-Lagrange equation. | ||
By plugging Iwer and | |||
By plugging Iwer and Silverstrawb's equation to solve for x and y, we obtain the parametric equations, the solution to the Iwerlipse after <math>n</math> frames: | |||
<math>x(n,t) = \pm \frac{v_xnt}{\sinh(t)} </math> | <math>x(n,t) = \pm \frac{v_xnt}{\sinh(t)} </math> | ||
| Line 33: | Line 34: | ||
[[Straining]] | [[Straining]] | ||
==References== | ==References== | ||
Proof of the optimal straining equation :<br> | |||
[[File:IwerlipseProof.png]] | |||
[[Category:Mechanics]] | [[Category:Mechanics]] | ||
Latest revision as of 11:29, 17 October 2024
The Iwerlipse is the range of positions Mario can occupy when Mario is in the air and cannot turn, assuming the joystick input polling were continuous. It is defined as an area bounded by a shape drawn by the solution to optimizing a set of 2 differential equations. Due to the shape being similar to a superellipse (after Grassdigger brute forced for the solution in Mathematica), Pannenkoek2012 proposed calling this shape the "Iwerlipse" on August 2018 (pronounced eeverlipse /ˈivɜlɪps/) as a pun on the name of Iwer Sonsch, one of the people involved in this problem.
The set of differential equations is:
f(t) is the function for a SM64 player's joystick tilt in terms of time.
a is forward acceleration, and is usually defined in game as 1.5.
vx is sideways velocity and is usually defined in game as 10.
D is drag, which usually can be values: +2.35, +0.35, 0, -0.35, -1.35. For TASing purposes, where high speed is always ideal, D is most commonly set to -1.35, for cases when Mario's forward speed is above 32.
The problem was posed by jongyon7192p as a curiosity, and it became relevant to the ABC challenge a few times before being solved through some other means.
Iwer stated on April 2018 that optimal straining for the Air_no_Turn action is .
On October 2019, Silverstrawb provided a full analytical proof for Iwer's claim, using a generalized 2nd-order Euler-Lagrange equation.
By plugging Iwer and Silverstrawb's equation to solve for x and y, we obtain the parametric equations, the solution to the Iwerlipse after frames:
![{\displaystyle {\frac {dx}{dt}}=v_{x}\cos[f(t)]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/143af62e6e561420b49f26819bb95a19653d5d94)
![{\displaystyle {\frac {d^{2}y}{dt^{2}}}=a\sin[f(t)]-D}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/966bcb400803c11c346090a271e3a6bfe29a0b49)